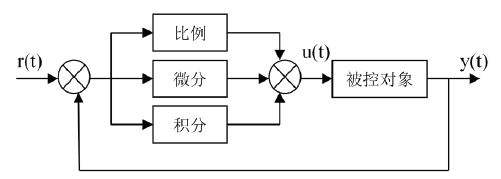
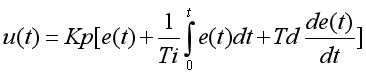三、平衡小车原理
平衡小车是通过两个电机控制两个轮子的转动抵消小车倾斜的倾角和倾角速度,使小车直立。
我们通过陀螺仪(MPU)来获取小车的倾角,角速度;霍尔编码器获取两个减速电机的转速和状态,STM32芯片处理数据并通过负反馈控制小车电机的转动来抵消小车的倾角。
角度(物理分析 PD算法)
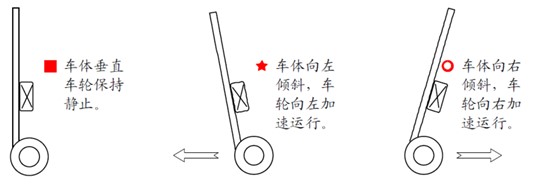
图1
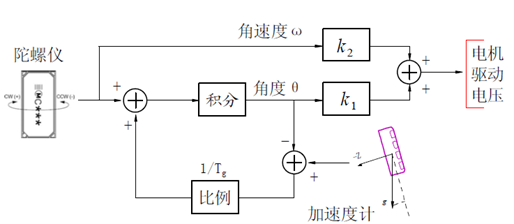
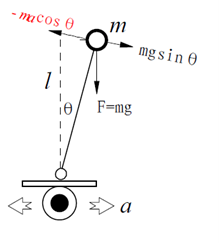
图2
·保持平衡:如图2所示,对小车做受力分析,小车因为重力的分量向前倾斜,这时候要恢复平衡的垂直位置,需要增加一个与mgsinθ方向相反的力使其保持平衡。因为θ很小,进行线性化。
F = mg sinA - ma cosA ≈ mgA - mk1 A
假设负反馈控制是加速度a与倾角A成正比,设a = k1A,当k1 > g 时,小车会产生一个回复力使小车回到垂直位置恢复平衡。
为了让小车尽快回到垂直位置稳定下来,还需要增加阻尼力。增加的阻尼力与偏角的速度成正比,方向相反。
F = mgA - mk1A - mk2A~
这个k2相当于给小车恢复力方向提供了一个加速度,让小车能够更快恢复垂直平衡位置,k2 = A~,A~为角加速度。
mgsinA反向作用力由小车车轮加速提供,所以小车车轮加速度的算法为:
a(t) = k1A + k2A~
图三是微分方程形式,线性化后会更好理解,不予赘述。

图3
在角度反馈控制中,与角度成比例的控制量是称为比例控制(Proportion 也就是PID算法中的P);与角速度成比例的控制量称为微分控制(角速度是角度的微分,Integral也就是PID算法中的I)。因此上面系数k1,k2分别称为比例和微分控制参数。其中微分参数相当于阻尼力,可以有效抑制车模震荡。通过微分抑制控制震荡的思想在后面的速度和方向控制中也同样适用。
总结控制车模直立稳定的条件如下:
(1)能够精确测量车模倾角θ的大小和角速度θ~的大小;
(2)可以控制车轮的加速度。
测速(物理模型 → 建立数学模型 传递函数 PD算法)
·上述控制实际结果是小车与地面不是严格垂直,而是存在一个对应的倾角,在实际小车制作过程中需要进行机械调整和软件参数设置。在重力的作用下,小车会朝着一个方面加速前进。为了保持小车的静止或者匀速运动需要消除这个安装误差,另外需要通过软件中的速度控制来实现速度的稳定性。在小车角度控制中出现的小车倾角偏差,使得小车在倾斜的方向上产生加速。这个结果可以用来进行小车的速度控制。下面将利用这个原理来调节小车的速度。
三个问题:
(1)如何测量小车速度?
(2)如何通过小车直立控制实现小车倾角的改变?
(3)如何根据速度误差控制小车倾角?
·第一个问题可以通过安装在电机输出轴上的光码盘来测量得到小车的车轮速度。如图4所示。利用控制单片机的计数器测量在固定时间间隔内速度脉冲信号的个数可以反映电机的转速。(霍尔编码器补充资料: 编码器计数原理与电机测速原理——多图解析 (zhihu.com)编码器计数原理与电机测速原理——多图解析 - 知乎 )
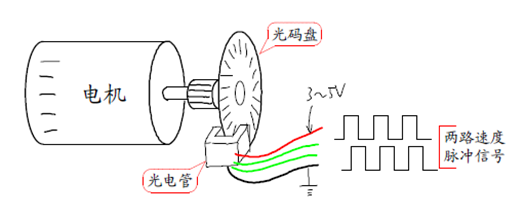
图4
·第二个问题可以通过角度控制给定值来解决。给定小车直立控制的设定值,在角度控制调节下,小车将会自动维持在一个角度。通过前面小车直立控制算法可以知道,小车倾角最终是跟踪重力加速度Z轴的角度。因此小车的倾角给定值与重力加速度Z轴角度相减,便可以最终决定小车的倾角
第三个问题分析起来相对比较困难,远比直观进行速度负反馈分析复杂。
·首先对一个简单例子进行分析。假设小车开始保持静止,然后增加给定速度,为此需要小车往前倾斜以便获得加速度。在小车直立控制下,为了能够有一个往前的倾斜角度,车轮需要往后运动,这样会引起车轮速度下降(因为车轮往负方向运动了)。由于负反馈,使得小车往前倾角需要更大。如此循环,小车很快就会倾倒。原本利用负反馈进行速度控制反而成了“正”反馈。(原因和解决方案狠复杂,我也看不懂,放在下边看得懂的看一下吧)
为什么负反馈控制在这儿失灵了呢?原来在直立控制下的小车速度与小车倾角之间传递函数具有非最小相位特性(在此省略了分析),在反馈控制下容易造成系统的不稳定性。
为了保证系统稳定,往往取的小车倾角控制时间常数Tz很大。这样便会引起系统产生两个共轭极点,而且极点的实部变得很小,使得系统的速度控制会产生的震荡现象。这个现象在实际参数整定的时候可以观察到。那么如何消除速度控制过程中的震荡呢?
要解决控制震荡问题,在前面的小车角度控制中已经有了经验,那就是在控制反馈中增加速度微分控制。但由于车轮的速度反馈信号中往往存在着噪声,对速度进行微分运算会进一步加大噪声的影响。为此需要对上面控制方法进行改进。原系统中倾角调整过程时间常数往往很大,因此可以将该系统近似为一个积分环节。将原来的微分环节和这个积分环节合并,形成一个比例控制环节。这样可以保持系统控制传递函数不变,同时避免了微分计算。
但在控制反馈中,只是使用反馈信号的比例和微分,没有利误差积分,所以最终这个速度控制是有残差的控制。但是直接引入误差积分控制环节,会增加系统的复杂度,为此就不再增加积分控制,而是通过与角度控制相结合后在进行改进。
要求小车在原地停止,速度为0。但是由于采用的是比例控制,如果此时陀螺仪有漂移,或者加速度传感器安装有误差,最终小车倾角不会最终调整到0,小车会朝着倾斜的方向恒速运行下去。注意此时车模不会像没有速度控制那样加速运行了,但是速度不会最终为0。为了消除这个误差,可以将小车倾角设定量直接积分补偿在角度控制输出中,这样就会彻底消除速度控制误差。第二点,由于加入了速度控制,它可以补偿陀螺仪和重力加速度的漂移和误差。所以此时重力加速度传感器实际上没有必要了。
此时小车在控制启动的时候,需要保持小车的垂直状态。此时陀螺仪的积分角度也初始化为0。当然如果电路中已经包括了重力加速度传感器,也可以保留这部分,从而提高小车的稳定性。在后面的最终给定的控制方案中,保留了这部分的控制回路
3.转向控制(PD算法)
通过左右电机速度差驱动小车转向消除小车距离道路中心的偏差。通过调整小车的方向,再加上车前行运动,可以逐步消除小车距离中心线的距离差别。这个过程是一个积分过程,因此小车差动控制一般只需要进行简单的比例控制就可以完成小车方向控制。但是由于小车本身安装有电池等比较重的物体,具有很大的转动惯量,在调整过程中会出现小车转向过冲现象,如果不加以抑制,会使得小车过度转向而倒下。根据前面角度和速度控制的经验,为了消除小车方向控制中的过冲,需要增加微分控制。
相关算法在4.全方案整合中。
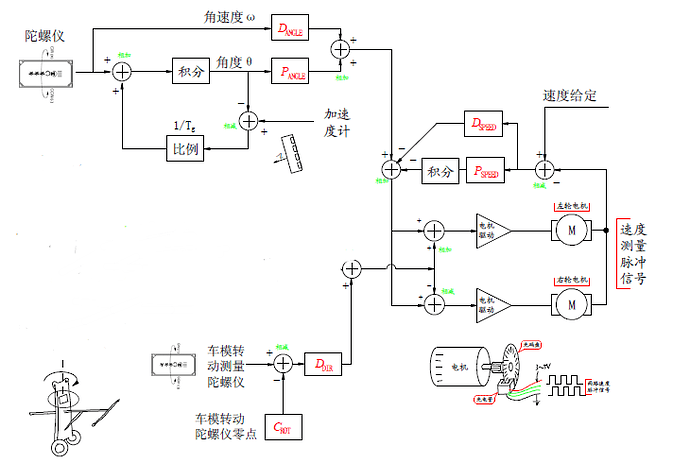
4.全方案整合
图5
需要采集的数据:
(1)陀螺仪信号:<1>小车倾角速度陀螺仪信号,获得小车的倾角和角速度
<2>小车转动速度陀螺仪信号,获得小车转向角速度
(2)重力加速的信号:用来补偿陀螺仪的漂移,在2.测速中有讲(加入了速度控制,它可以补偿陀螺仪和重力加速度的漂移和误差。所以此时重力加速度传感器实际上没有必要了),该信号可以忽略
(3)电机转速脉冲信号:通过霍尔编码器获得小车电机转速反馈得到小车运动速度,进行方向控制
在<平衡><测速><方向控制>三个环节中,都使用了<比例微分>(PD)控制,这三种算法的输出量最后通过叠加通过电机运动完成。
5.PID算法(PID算法快速扫盲:简易PID算法的快速扫盲(超详细+过程推导+C语言程序) - 知乎 )
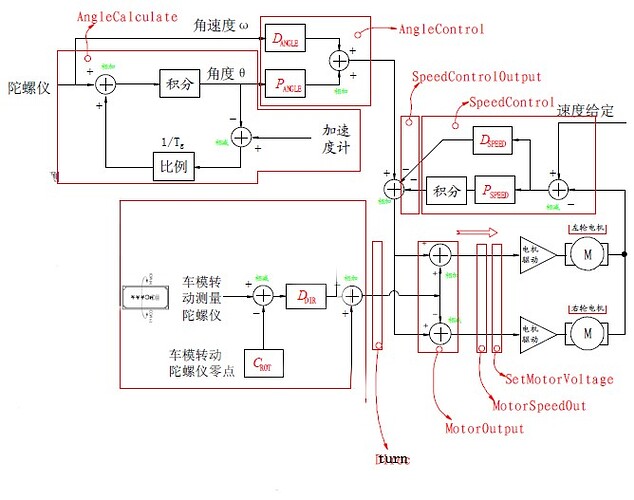
图6
控制相关的软件函数包括:
1.AngleCalculate :小车倾角计算函数。根据采集到的陀螺仪和重力加速度传感器的数值计算小车角度和角速度。如果这部分的算法由外部一个运放实现,那么采集得到的直接是小车的角度和角速度,这部分算法可以省略。该函数是每5毫秒调用一次。
2.AngelControl :小车直立控制函数。根据小车角度和角速度计算小车电机的控制量。直立控制是5毫秒调用一次。
3.SpeedControl :小车速度控制函数。根据小车采集到的电机转速和速度设定值,计算电机的控制量。该函数是40毫秒调用一次。
4.MotorOutput :电机输出量汇集函数。根据前面的直立控制、速度控制和方向控制所得到的控制量进行叠加,分别得到左右两个电极的输出电压控制量。对叠加后的输出量进行饱和处理。函数调用周期5毫秒。在此请大家注意速度控制量叠加的极性是负。
5.MotorSpeedOut:电机PWM输出计算函数。根据左右两个电极的输出控制量的正负极性,叠加上一个小的死区数值,克服车模机械静态摩擦力。函数调用周期5毫秒。
6.SetMotorVoltage:PWM输出函数:根据两个电机的输出量,计算出PWM控制寄存器的数值,设置四个PWM控制寄存器的数值。函数调用周期1毫秒。
7.Chaoshengbo: 加入超声波避障模块:根据前方障碍物的距离检测,一旦检测到后,通过直接PWM值输出( g_fchaoshengbooutput),相障碍物反方上运动,无需算法实现。每30毫秒调用一次。
算法:
(1)小车直立控制:使用小车倾角的PD(比例、微分)控制;
g_fAngleControlOut = g_fCarAngle * g_fCarAngle_P + gyro[0] * g_fCarAngle_D ;
【编者注】:a = k1 * A + k2 * A~,
AngleControlOut:表示电机角度控制的输出,就是电机的运动量
CarAngle_P:表示电机角度的比例k1
CarAngle_D:表示小车角度的比例k2
CarAngle: 表示此时小车的倾斜角度
gyro[0]: 表示角速度
小车速度控制:使用PD(比例、微分)控制;
g_fSpeedControlOutNew = (CAR_SPEED_SET - g_fCarSpeed) * g_fCarSpeed_P
(CAR_POSITION_SET - g_fCarPosition) * g_fCarSpeed_I;
【编者注】:速度控制更新 = (设定的小车速度 - 此时小车的速度) * 小车速度的比例 +
(设定的小车位置 - 此时小车的位置) * 小车速度的积分
小车方向控制:使用PD(比例、微分)控制。
*speednow=-speedtarget*3.4 -gyro[2]0.0015 ;
【编者注】:现在的速度 = -设定速度 * 3.4 - (这个gyro像是陀螺仪返回数据,我也不太清楚) * 0.0015
在上面控制过程中,车的角度控制和方向控制都是直接将输出电压叠加后控制电机的转速实现的。而车的速度控制本质上是通过调节车模的倾角实现的,由于车是一个非最小相位系统,因此该反馈控制如果比例和速度过大,很容易形成正反馈,使得车失控,造成系统的不稳定性。因此速度的调节过程需要非常缓慢和平滑。