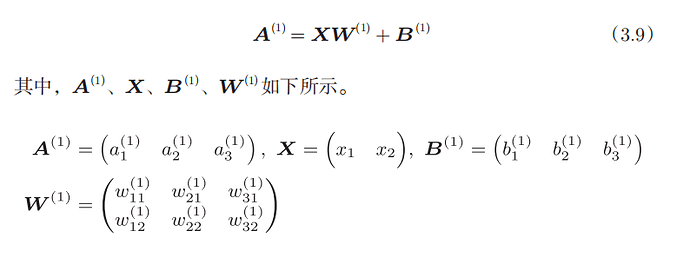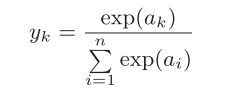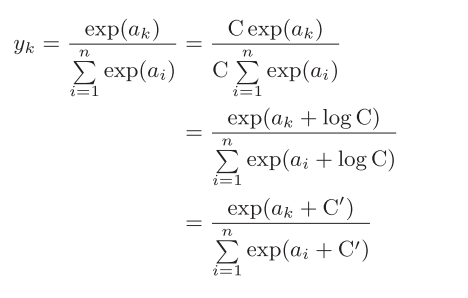对于复杂的函数,感知机也有表示它的可能性,但是需要人工设定权重
神经网络则可以自动从数据中学习到合适的权重参数
3.1从感知机到神经网络
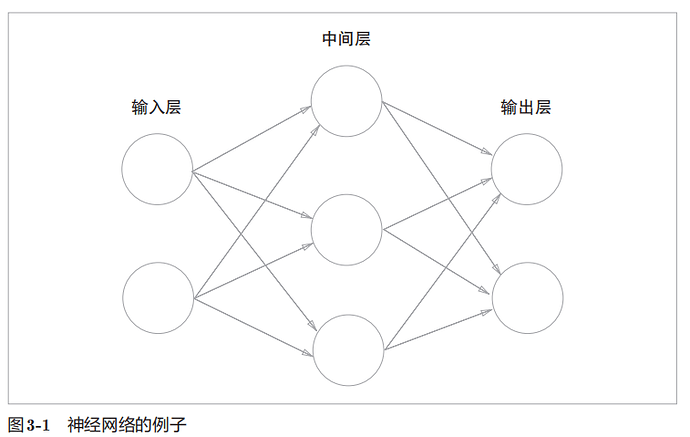
神经网络的例子:
输入层:第0层 中间层:第1层 输出层:第2层
可以称为3层网络,也可以称为2层网络,输出层没有权重
复习感知机
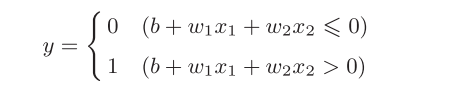
b是被称为偏置的参数,用于控制神经元被激活的容易程度;
而w1和w2是表示各个信号的权重的参数,用于控制各个信号的重要性
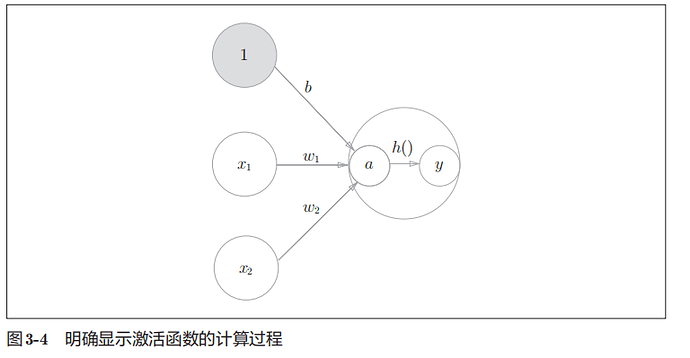
为了简化式子,我们引入新函数h(x)
y = h(b + w1x1 + w2x2)
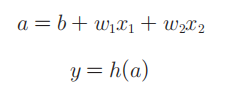
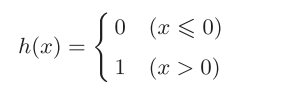
即信号的加权总和为节点a,然后节点a被激活函数h()转换成节点y
h(x)函数会将输入信号的总和转换为输出信号,这种函数一般称为激活函数
一般而言:“朴素感知机”指单层网络:激活函数使用阶跃函数模型
“多层感知机”指神经网络:使用sigmoid函数
3.2激活函数
sigmoid函数
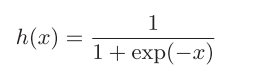
一维感知机使用阶跃函数作为激活函数,而神经网络使用sigmoid函数
阶跃函数的实现

x>0:传入的numpy数组与0比较,结果为bool型数组,dtype.int将bool转换为0或1;最后返回numpy数组
np.arange(-5.0, 5.0, 0.1)在−5.0到5.0的范围内,以0.1为单位,生成NumPy数组([-5.0, -4.9, …, 4.9])
sigmoid函数的实现
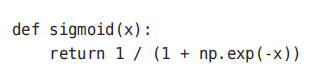
根据numpy数组的广播功能,1 / (1 + np.exp(-x))的运算将会在NumPy数组的各个元素间进行

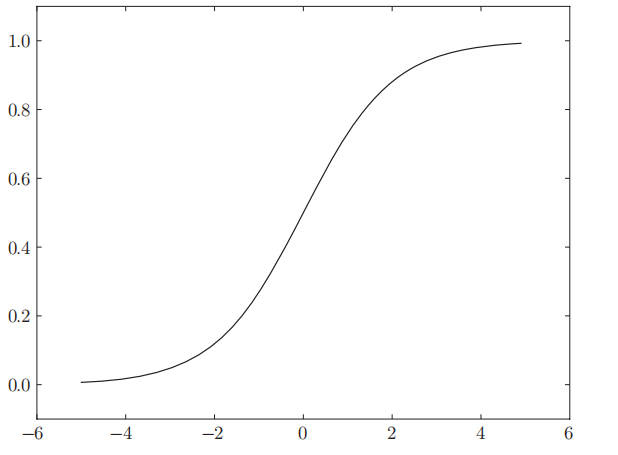
sigmoid和阶跃函数的比较
不同
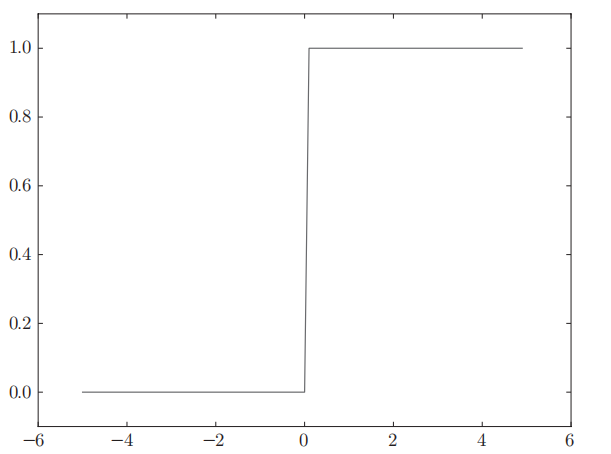
1.sigmoid函数是一条平滑的曲线,输出随着输入发生连续性的变化。
而阶跃函数以0为界,输出发生急剧性的变化。
2.感知机中神经元之间流动的是0或1的二元信号,
而神经网络中流动的是连续的实数值信号(即阶跃函数只能返回0或1,而sigmoid可以返回更多实数)
相同
1.结构均是“输入小时,输出接近0(为0);随着输入增大,输出向1靠近(变成1)”。
也就是说,当输入信号为重要信息时,都会输出较大的值;
当输入信号为不重要的信息时,两者都输出较小的值。
2.还有一个共同点是,不管输入信号有多小,或者有多大,输出信号的值都在0到1之间
非线性函数
阶跃函数和sigmoid函数都是非线性函数,神经网络的激活必须使用非线性函数,若用线性函数加深神经网络式没有意义的。比如一次函数y=cx加深多层,也仅仅是系数取了次方,可以用单层来替代
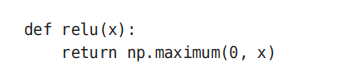
RELU函数
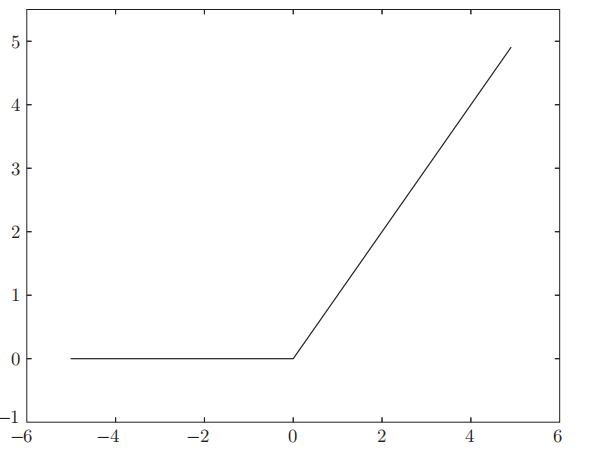
ReLU函数在输入大于0时,直接输出该值;在输入小于等于0时,输出0
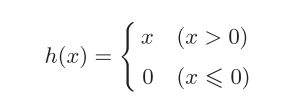
3.3 多维数组的运算

这里提到了数组的维数,也没有太明白,暂且理解为一个下标就能访问的数组
数组的维数可以通过np.dim()函数获得
数组的形状可以通过实例变量shape获得

一个3 × 2的数组表示,第一个维度有3个元素,第二个维度有2个元素,我理解为3行2列
第一个维度对应第0维,第二个维度对应第1维(索引从0开始)
二维数组也称为矩阵
矩阵乘法
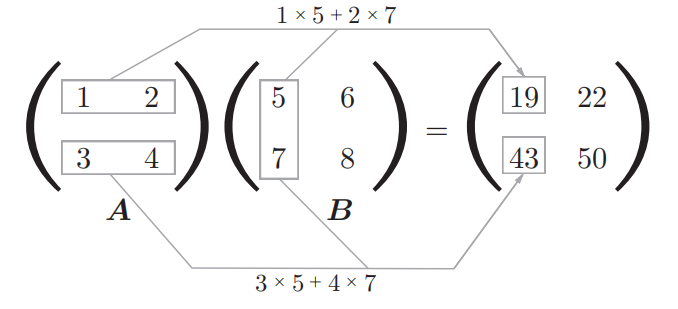
与线性代数相同,相乘时采用左行右列法。需要满足第一个矩阵的列数==第二个矩阵的行数
乘积可以通过 NumPy 的np.dot()函数计算
![]()
3.4 3层神经网络的实现
前向处理:从输入到输出
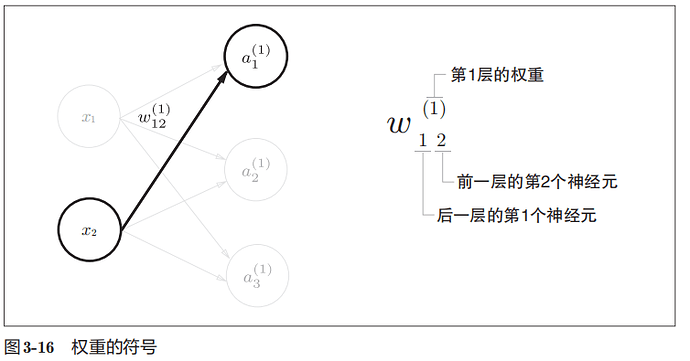
下图给出了神经网络中符号的含义
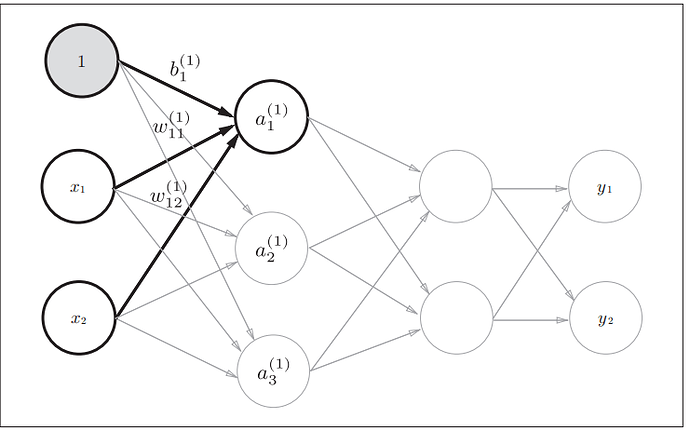
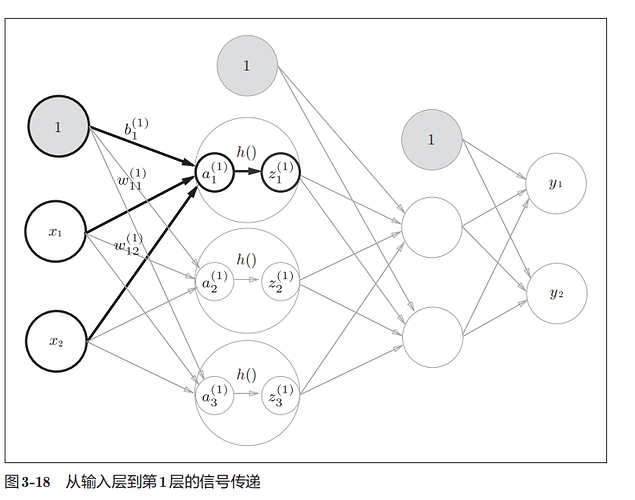
下图给出了各层间信号传递的实现
偏置的右下角的索引号只有一个。这是因为前一层的偏置神经元(神经元“1”)只有一个
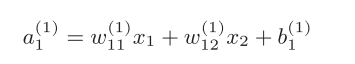
第1层的每个神经元=激活函数【(上层的神经元*权重)求和+偏置】
如果使用矩阵的乘法运算
将输入信号简化之后就可以表示为下图,输入信号用a表示,经过激活函数h得到z
这里看似很复杂,我个人感觉就是一系列的代数运算,每一个神经元的输入、权重、偏置不同
3.5 输出层的设计
机器学习可分为分类问题和回归问题
分类问题:数据属于哪一类
回归问题:根据某个输入预测一个数值
一般而言,回归问题用
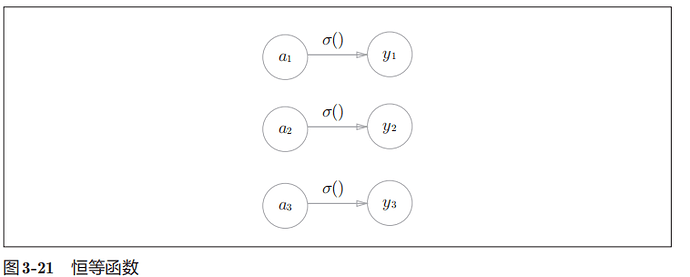
1.回归问题用恒等函数
恒等函数:输入==输出,无任何改动
2.分类问题用softmax函数
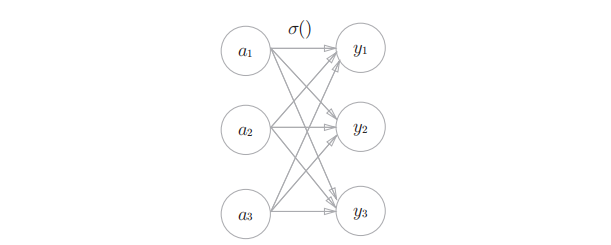
假设输出层共有n个神经元,计算第k个神经元的输出yk
softmax函数的分子是输入信号ak的指数函数,分母是所有输入信号的指数函数的和
问题:由于进行指数运算,值容易变得非常大,就会溢出
改进:
这个C对于原函数来说是没有任何影响的,c‘ 可以使用任何值,但是为了防止溢出,一般会使用输入信号中的最大值,Ak减去c‘时,指数次幂就会缩小,可计算。
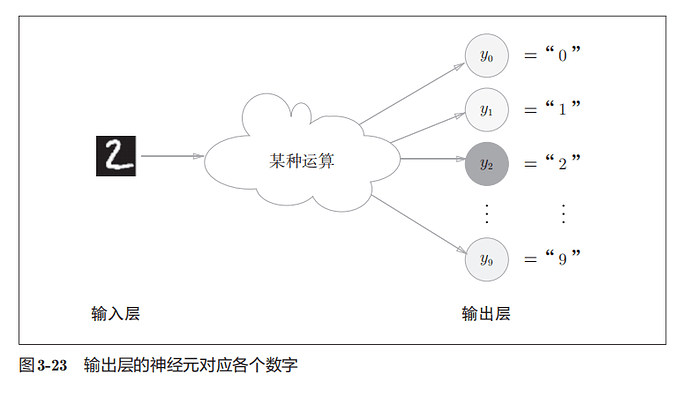
使用softmax元素并没有改变各个元素的大小关系,指数为单增的,,神经网络只把输出值最大的神经元所对应的类别作为识别结果
y2输出的值最大,颜色最深,代表神经网络预测的是y2对应的类别
求解机器学习问题的步骤可以分为“学习” 和“推理”两个阶段,先在学习阶段进行模型的学习,然后在推理阶段,用学到的模型对未知的数据进行推理(分类