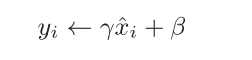6.1参数的更新
神经网络的学习的目的是找到使损失函数的值尽可能小的参数,把这个寻找最优参数的过程称为最优化。但是,神经网络的参数空间非常复杂,参数量也十分庞大,优化问题就变得复杂。
前面讲到了随机梯度下降法SGD,
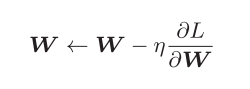
使用参数的梯度,沿梯度方向更新参数,并重复这个步骤多次,从而逐渐靠近最优参数。
w:需要更新的权重参数, :损失函数关于w的梯度 η:学习率
:损失函数关于w的梯度 η:学习率
我们用上式右边的值更新左边的值
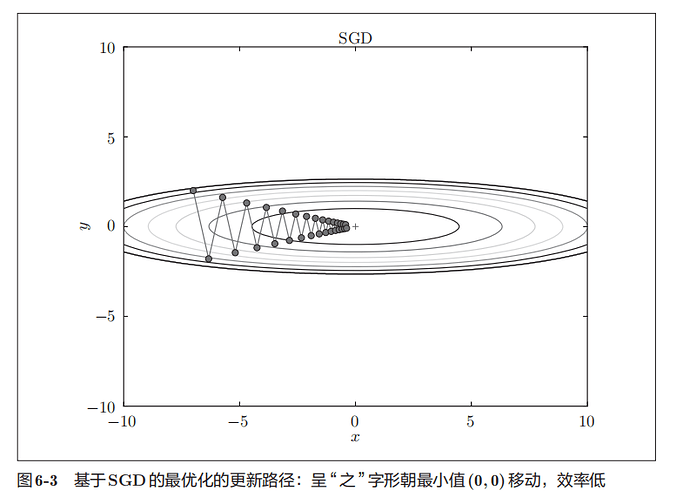
虽然SGD简单,但解决某些问题缺乏效率
比如在上图中,搜索路径呈’之‘形移动,根本原因是梯度的方向只是当前变化最大的方向,而不是指向最小值的方向。
6.1.4 momentum
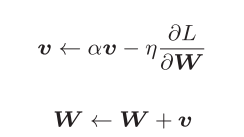
这里新出现了一个变量v,对应物理上的速度
第一个式子表示了在里的作用下速度改变的法则,α<1,在物体不受力时使其逐渐减速
和SGD相比,我们发现“之”字形的“程度”减轻了
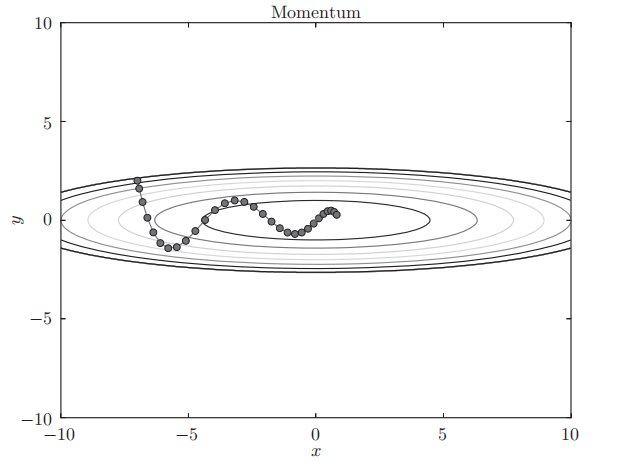
x方向一直受同一方向的力,有加速。y方向交互收到正方向和反方向的力,互相抵消,所以y轴上速度不稳定,可以减弱之字形变动程度
6.1.5 AdaGrad
学习率过小,会导致学习花费过多时间;反过来,学习率过大,则会导致学习发散而不能正确进行。于是乎,提出了一种学习率衰减的有效技巧。即随着学习的进行,使学习率逐渐减小,一开始”多学“,逐渐”少学“。
逐渐减小学习率的想法,相当于将“全体”参数的学习率值一起降低。而adagrad发展了这个方法,会为参数的每个元素适当地调整学习率。
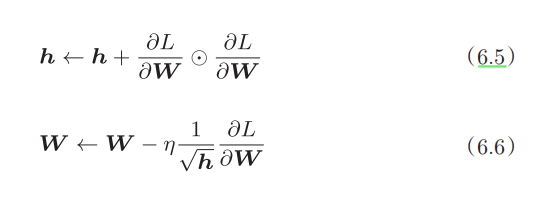
新变量h,保存了以前的所有梯度值的平方和(表示对应矩阵元素的乘法)。在更新参数时,通过乘以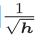 ,就可以调整学习的尺度。参数的元素中变动较大(被大幅更新)的元素的学习率将变小。
,就可以调整学习的尺度。参数的元素中变动较大(被大幅更新)的元素的学习率将变小。
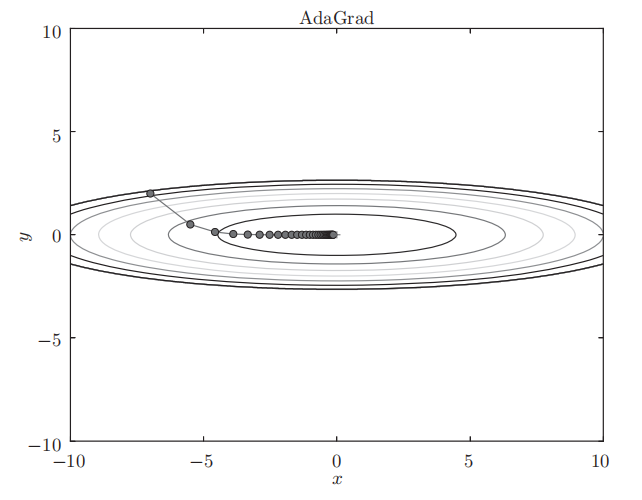
y轴梯度较大,刚开始变化大,逐渐减小更新的步伐,y轴更新程度减弱,”之“字形变动程度衰减。
6.1.5 Adam
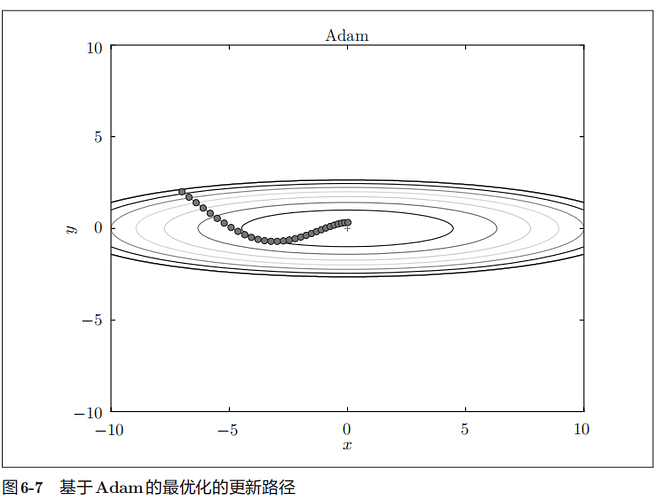
Momentum参照小球在碗中滚动的物理规则进行移动,AdaGrad为参数的每个元素适当地调整更新步伐。adam结合二者的有点,实现参数空间的高效搜索
6.2权重的初始值
我们想通过减小权重参数的值来抑制过拟合的发生,那把它设为0如何?
比如,在2层神经网络中,假设第1层和第2层的权重为0。这样一来,正向传播时,因为输入层的权重为0,所以第2层的神经元全部会被传递相同的值。这意味着反向传播时第2层的权重全部都会进行相同的更新,这使得神经网络拥有许多不同的权重的意义丧失了。
所以需要随机生成初始值
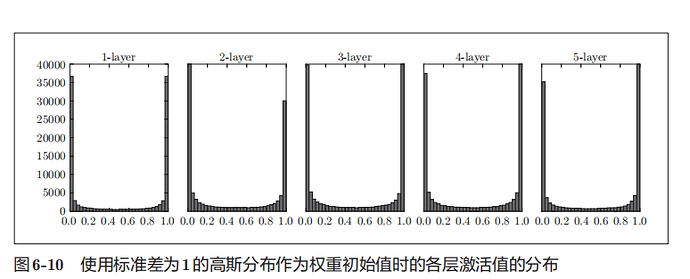
用标准差为1的高斯分布随机生成1000个数据作为输入数据,并把它们传给5层神经网络。激活函数使用sigmoid函数。
各层激活值的分布图:
sigmoid函数是s型函数,输出靠近0或1的时候,导数值接近0.所以偏向0和1的数据分布会造成反向传播中梯度的值不断变小,最后消失。这个问题称为
梯度消失。
将输入改为标准差为0.01的高斯分布
这次呈集中在0.5附近的分布,不会发生梯度消失了。但是激活值还是
有所偏向,
而我们希望激活值的分布有适当的广度,各层传递多样的数据,神经网络才能进行高效的学习。
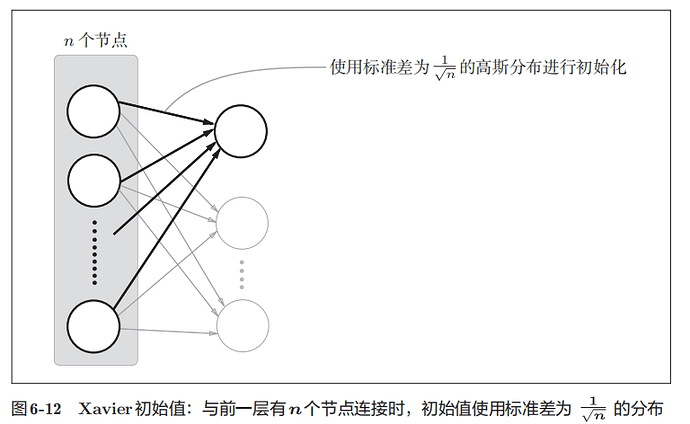
于是引入了Xavier初始值
为了使各层的激活值呈现出具有相同广度的分布, 推导出的结论是,如果前一层的节点数为n,则初始值使用标准差为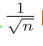 的分布
的分布
前一层的节点数越多,要设定为目标节点的初始值的权重尺度就越小
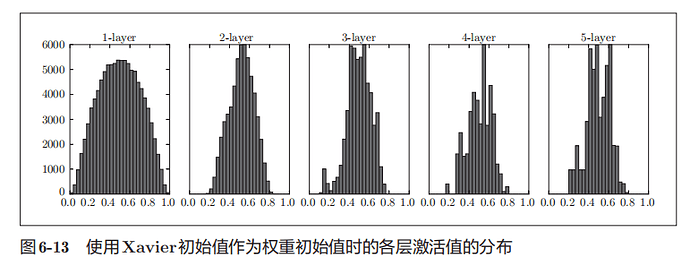
使用Xavier初始值进行实验
越是后面的层,图像变得越歪斜,但是呈现了比之前更有广度的分布,各层间传递的数据有适当的广度,有望进行高效的学习
6.2.3relu的权重初始值
sigmoid函数和tanh函数左右对称,且中央附近可以视作线性函数,所以适合使用Xavier初始值。而relu适合使用“He初始值”。
当前一层的节点数为n时,He初始值使用标准差为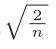 的高斯分布
的高斯分布
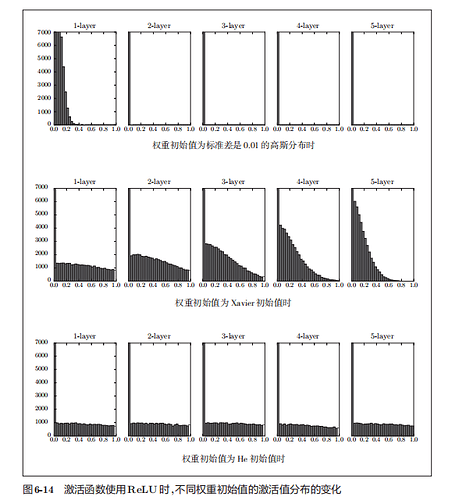
下面对比了使用relu函数时,激活值的分布:
图1知,用0.01标准差的高斯分布时,各层的平均激活值非常小,故神经网络上传递的是非常小的值,说明逆向传播时权重的梯度也同样很小,学习就会没什么进展
图2知,随着层的加深,偏向一点点变大,则学习时会出现梯度消失的问题
图3知,而当初始值为He初始值时,各层中分布的广度相同。即便层加深,数据的广度也能保持不变,因此逆向传播时,也会传递合适的值。
当激活函数使用ReLU时,权重初始值使用He初始值,当激活函数为sigmoid或tanh等S型曲线函数时,初始值使用Xavier初始值。
6.3batch normalization
如果设定了合适的权重初始值,则各层的激活值分布会有适当的广度,从而可以顺利地进行学习
Batch Normalization方法“强制性”地调整激活值的分布,使其各层拥有适当的广度。
为此,要向神经网络中插入对数据分布进行正规化的层,即Batch Normalization层,具体而言,就是进行使数据分布的均值为0、方差为1的正规化。
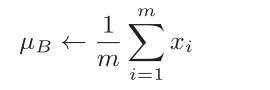 求均值
求均值
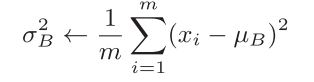 求方差
求方差
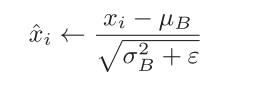 正规化
正规化
将这个处理插入到激活函数的前面(或者后面),可以减小数据分布的偏向
接着,Batch Norm层会对正规化后的数据进行缩放和平移的变换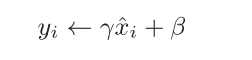
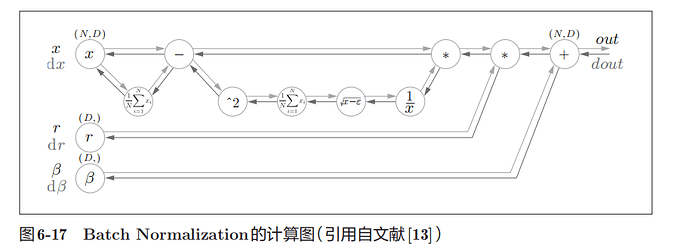
Batch Norm可以表示为图:
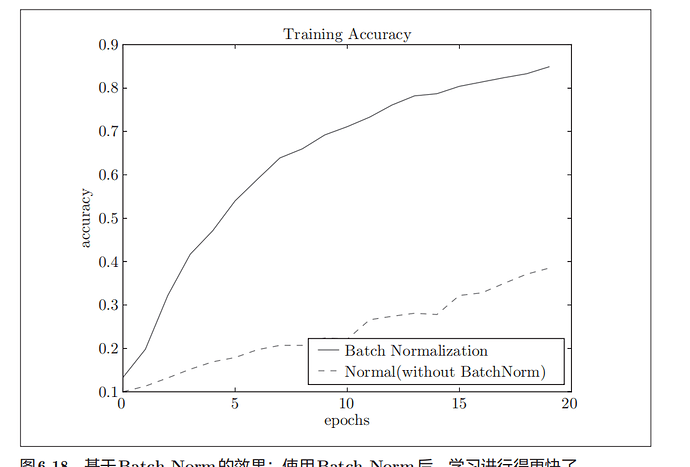
根据实验结果,使用batch norm之后,学习进行得更快了
6.4正则化
机器学习的问题中,过拟合是一个很常见的问题。过拟合指的是只能拟合训练数据,但不能很好地拟合不包含在训练数据中的其他数据的状态。机器学习的目标是提高泛化能力
发生过拟合的原因:

故意满足这两个条件
可以发现,对于测试数据,模型的拟合效果不是很好。
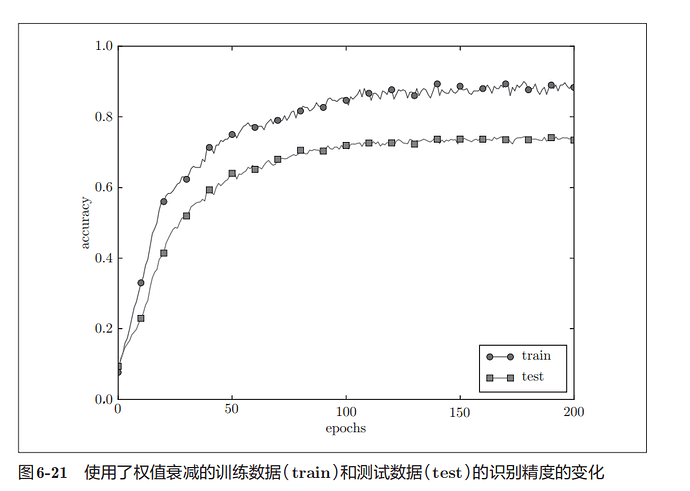
6.4.2权值衰减
权值衰减是经常被使用的抑制过拟合的方法。通过在学习的过程中对大的权重进行惩罚,来抑制过拟合。
神经网络的学习目的是减小损失函数的值,通过给损失函数加上权重的平方范数来实现,可以抑制权重变大。
权重记为W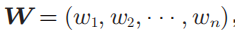 ,L2范数
,L2范数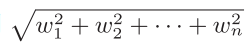
L2范数的权值衰减就是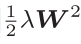 ,λ是控制正则化强度的超参数。λ设置得越大,对大的权重施加的惩罚就越重。将其加到损失函数上。
,λ是控制正则化强度的超参数。λ设置得越大,对大的权重施加的惩罚就越重。将其加到损失函数上。
对于所有权重,权值衰减方法都会为损失函数加上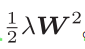 ,求权重梯度时,要为之前的误差反向传播法的结果加上正则化项的导数λW。
,求权重梯度时,要为之前的误差反向传播法的结果加上正则化项的导数λW。
应用λ = 0.1的权值衰减,可以发现,于没有使用权值衰减的结果相比,差距变小了,过拟合收到了抑制。
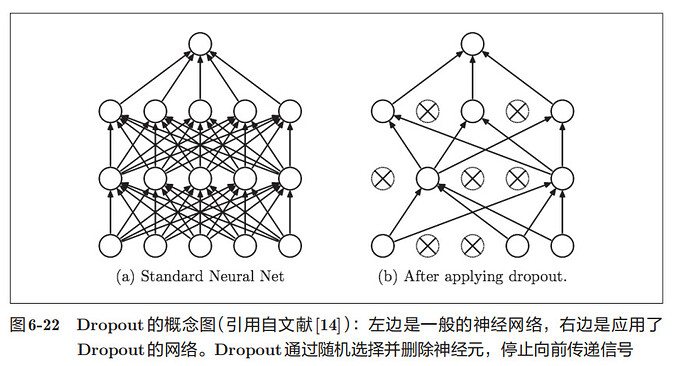
6.4.3Dropout
如果网络的模型变得很复杂,只用权值衰减就难以应对了。这里使用了Dropout方法
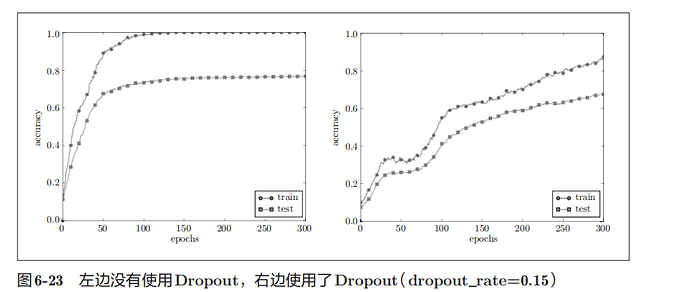
Dropout是一种在学习的过程中随机删除神经元的方法。训练时,随机选出隐藏层的神经元,然后将其删除。被删除的神经元不再进行信号的传递。训练时,每传递一次数据,就会随机选择要删除的神经元。测试时,虽然会传递所有的神经元信号,但是对于各个神经元的输出,要乘上训练时的删除比例后再输出
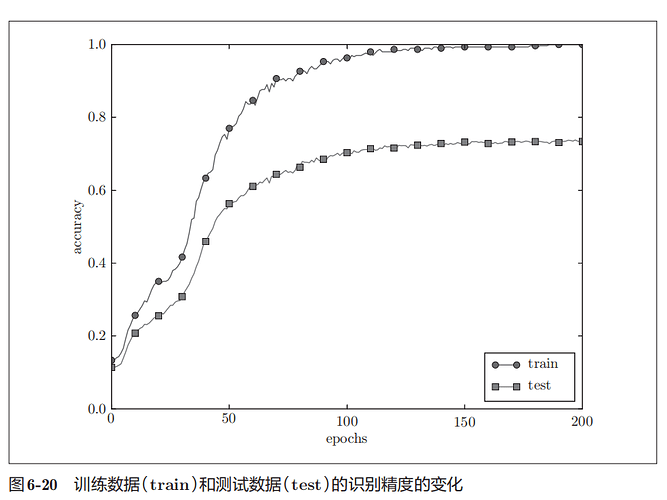
通过使用Dropout,训练数据和测试数据的识别精度的差距进一步变小了
1 个赞
超参数的验证
神经网络中,除了权重和偏置等参数,超参数(hyper-parameter)也经常出现,比如各层的神经元数量、batch大小、参数更新时的学习率或权值衰减等
我们要对超参数设置各种各样的值以进行验证,但是不能使用测试数据评估超参数的性能。用测试数据确认超参数的值的“好坏”,就会导致超参数的值被调整为只拟合测试数据。
调整超参数时,必须使用超参数专用的确认数据,即验证数据
超参数的最优化
如何优化超参数呢?
进行超参数的最优化时,逐渐缩小超参数的“好值”的存在范围。所谓逐渐缩小范围,是指一开始先大致设定一个范围,从这个范围中随机选出一个超参数(采样),用这个采样到的值进行识别精度的评估;然后,多次重复该操作,观察识别精度的结果,根据这个结果缩小超参数的“好值”的范围。
1 个赞
但是这个方法会导致自变量在梯度值较小的维度上迭代较慢
因为h是一直在累加的,所以他的学习率会一直减小,问题是,当梯度较大的时候,我们要继续学习,而学习率较低,学不起来怎么办?一个办法就是我们的梯度只计算当前位置附近的,而对于较远位置的梯度,我们则选择遗忘。
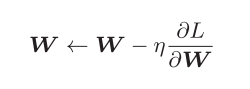
![]() :损失函数关于w的梯度 η:学习率
:损失函数关于w的梯度 η:学习率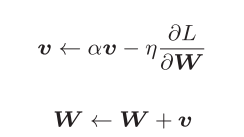

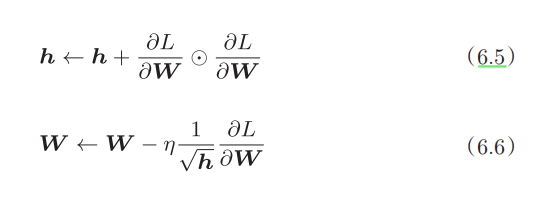
![]() ,就可以调整学习的尺度。参数的元素中变动较大(被大幅更新)的元素的学习率将变小。
,就可以调整学习的尺度。参数的元素中变动较大(被大幅更新)的元素的学习率将变小。

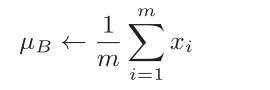 求均值
求均值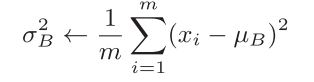 求方差
求方差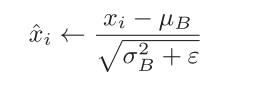 正规化
正规化