第四章
由神经网络的学习方式引入,可以直接学习图像本身,包含重要的特征量。将数据分为训练数据和测试数据,用训练数据进行学习,用测试数据评价模型的泛化能力。
学习的效果以损失函数为指标,可以通过均方误差和交叉熵误差来表示,更新权重参数,使损失函数的值越小越好。当数据量过大,全部计算损失函数就不太现实,可以从全部数据中选出一部分作近似,对这批数据进行学习,即mini-batch学习。
要找到损失函数的最小值,可以使用梯度法,函数的取值从当前位置沿着梯度方向前进一定距离,然后在新的地方重新求梯度,再沿着新梯度方向前进, 如此反复,不断地沿梯度方向前进。
第五章
但是数值微分或者梯度法比较浪费时间,于是提出了一种更加高效计算权重参数梯度的方法—误差反向传播法。
先由计算图引入,计算图就是将计算的各个步骤做拆分,反向计算的时候就可以很清楚的知道前一步的计算。反向传播局部导数的原理是**链式法则,**类似复合函数求偏导数的过程。后面分别讲述了加法节点、乘法节点的反向传播。此后讲述了激活函数层,包括relu,sigmoid层的求复合函数求偏导的过程
第六章
但是随机梯度下降法,梯度只是当前位置变化最大的方向,而并不是直接走向最小值的方向,走出来为之字形,解决某些问题就缺乏效率。引入了momentum的方法,
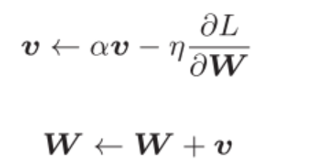
当梯度较小时,学习率较小,那参数的变化较小,梯度较大时,学习率变大,参数变化则增大,样就可以解决sgd方法的问题。
学习率过小,会导致学习花费过多时间;反过来,学习率过大,则会导致学习发散而不能正确进行。于是引入了adagrad方法 。
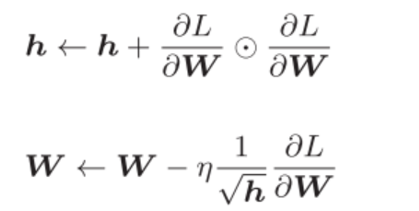
H表示梯度值的平方和,随着不断学习,h会逐渐增大,学习率会逐渐减小,以调整学习的尺度。
但是这样就产生了一个问题,因为h是一直在累加的,所以他的学习率会一直减小,当梯度较大的时候,我们要继续学习,而学习率较低,学不起来。则我们的梯度和只计算当前位置附近的,而对于较远位置的梯度,选择遗忘。
此后讲到了权重的初始值的问题,对于sigmoid函数,使用Xavier初始值,relu函数初始值使用标准差为的高斯分布。
为了使激活值分布有适当的广度,可以用batch normalization强制调整激活值的分布,使得学习进行的更快。
正则化方面,过拟合是一个常见的问题,我们要提高模型的泛化能力,可以通过权值衰减的方法抑制过拟合,对于复杂的模型,则可以使用dropout方法